Run a map-based surface water simulation model on the Niger River Basin in West Africa and demonstrate several graphical analysis tools available with the model. The input rainfall data and runoff data for model calibration have already been prepared for this area and provide reasonable results.
This exercise requires Arcview Version 2.0 or 2.1. The data needed for this exercise have already been loaded onto the PC's you will be using and may be found under the directory \gisfiles\ex4af\ngflow.
To get started, start ArcView and open the Project called ngflow.apr . Open the View Niger and you will see the river line and watershed polygon maps used in the model. Eight Themes should exist in the View Niger. A brief description of these Themes is provided here:
A simulation run using 90 months of data from July 1983 to December 1990 has already been made. The first part of this exercise will show you how to take a look at some of inputs and outputs from this model run. After that, a smaller sub-model will be cut out and you will be able to run a simulation model and optimization model on a smaller area. This is done so you do not have to wait too long while the simulation of the entire basin is made.
Surplus values are the input data to the surface water simulation model.
Surplus is excess rainfall that is available for streamflow generation.
Surplus values used here are the result of soil-water balance calculations.
A Table that contains a time-series of 90 surplus values for each sub-watershed
in the map is available. To make a graph of the surplus time-series at
a watershed of your choice, click on ![]() .
At the first menu, enter 1 to indicate that you wish to plot a time-series
at a location. Click OK and then click on any sub-watershed in the map.
Note: The watersheds in the lower third of the map receive much more
rainfall than watersheds towards the top of the map. If you click on a
watershed near the top of the map, you may see little or no surplus. At
the next menu, select "psurp.dbf" as the Table to plot and click
OK. Click YES to keep the chart and then OK to give the chart a default
name. You will be asked whether you want to plot data from another time
series table for the same location. Click NO. Click on another location
on the map, select "psurb.dbf" again as the table to plot, click
OK, keep the chart (YES), name the chart (OK), and click NO when asked
to plot another table.
.
At the first menu, enter 1 to indicate that you wish to plot a time-series
at a location. Click OK and then click on any sub-watershed in the map.
Note: The watersheds in the lower third of the map receive much more
rainfall than watersheds towards the top of the map. If you click on a
watershed near the top of the map, you may see little or no surplus. At
the next menu, select "psurp.dbf" as the Table to plot and click
OK. Click YES to keep the chart and then OK to give the chart a default
name. You will be asked whether you want to plot data from another time
series table for the same location. Click NO. Click on another location
on the map, select "psurb.dbf" again as the table to plot, click
OK, keep the chart (YES), name the chart (OK), and click NO when asked
to plot another table.
You can also plot graphs of the simulated flow time series in the river at either the to-node (upstream end of a specified reach) or from-node (downstream end of a specified reach). This is done using essentially the same procedure described above. Graphs of this type can be used to see that some of the reaches in the Niger Basin are "gaining" reaches and some are losing "reaches." Here is a procedure that you can follow to see the "from flow" and "to flow" along two reaches of this type. An image is included here to help you locate these two reaches. The reach with grid-code 448 is a gaining reach and the reach with grid-code 1969 is a losing reach.

Click on ![]() , enter option 1
, and click OK. Click on subwatershed 448, select "fflow.dbf",
and click OK. Keep the chart by clicking YES, click OK for the chart name,
and click YES to use another time series table for plotting. Select "tflow.dbf"
and click OK, click YES and OK and then NO. It will probably be helpful
to resize the chart windows with the mouse so the results can be seen more
easily. Looking at these results, it is clear that this reach is a gaining
reach because the downstream (tflow) values are higher than the upstream
values (fflow). Be careful when looking at these graphs because the x-axis
scales are automatically adjusted to reflect the range of values. On the
x-axis, "J" is July and "D" is December. Repeat the
same procedure to look at the graphs for the watershed with grid-code 1969
and you will see that this is a losing reach.
, enter option 1
, and click OK. Click on subwatershed 448, select "fflow.dbf",
and click OK. Keep the chart by clicking YES, click OK for the chart name,
and click YES to use another time series table for plotting. Select "tflow.dbf"
and click OK, click YES and OK and then NO. It will probably be helpful
to resize the chart windows with the mouse so the results can be seen more
easily. Looking at these results, it is clear that this reach is a gaining
reach because the downstream (tflow) values are higher than the upstream
values (fflow). Be careful when looking at these graphs because the x-axis
scales are automatically adjusted to reflect the range of values. On the
x-axis, "J" is July and "D" is December. Repeat the
same procedure to look at the graphs for the watershed with grid-code 1969
and you will see that this is a losing reach.
To demonstrate the simulation and optimization capabilities of the model, it is easier to cut out a sub-model from the big model to speed up computations. To create a usable sub-model,

You cannot see the point representing the Koulikoro station in this figure because it is highlighted. After completing your selection, make sure that "Mrunoff," "Dams.shp," "Flowchk.shp," "Ngriver.shp," and "Ngbasin.ply" are still the active Themes.
You probably will want to enlarge View1 that contains your sub-model and looks something like this:

Go ahead and close the view "Niger" because you will not be needing this view for the remainder of this exercise. To run the simulation model, make sure that the view containing your sub-model is active and choose the option SFwModel/SFlowSim from the pull down menus. You will then be given the option to specify some parameters for the simulation run. Here is a description of the parameters set at this menu:
Leave these parameters as they are and click OK to run the simulation. River arcs are highlighted as computations are made.
The basic steps in the flow routing algorithm are to first transform the surplus data on each subwatershed to a local runoff (Pflow) contribution. This is done using a response function. Several options are available in the program for routing the flow through the river network. Among these options are a response function approach, the Muskingum Cunge routing method, and a two-step flow routing approach. The two-step flow routing model is a special case of the response function routing model. The two step model is the default model that gets implemented when a user supplied response function is not available or when the Muskingum method is not computationally efficient. The basic equation for the two-step routing model is given here:
![]()
In this equation, Llagi is the normalized time lag between the from-node and to-node of river section i. Llagi is defined by:

Dflow is the diversion which is zero in this case. Li is the length
of river section i, vi is the average flow velocity on river section i
(m/s), and t is the time step. Let's look at an example of where the program
gets the numbers to make this calculation. First, make the Theme Ngriver.shp
active and click on ![]() to see the
attributes of Ngriver.shp. Select the record with grid-code 441 and note
that the "velocity" is 0.15 m/s, the "LossC" is 0.001
(1/km), and the "Length" is 85083 m. The loss coefficient is
0.001/1000 or 0.000001 in (1/m). These numbers can be used to calculate
a Llag for the river segment 441. The time step for calculations is equal
to the number of seconds in a month or 86400*365/12=2628000. The LLag is
then 85083/0.15/2628000 = 0.2158. To get the FFlow(t) and Fflow(t-1), open
the table "fflow.dbf" and take a look. Scroll to the right until
you find the field "gc441". Let's make a calculation for t=90
so scroll all the way to the bottom of the "fflow" table and
look at the last record. You should see something like this:
to see the
attributes of Ngriver.shp. Select the record with grid-code 441 and note
that the "velocity" is 0.15 m/s, the "LossC" is 0.001
(1/km), and the "Length" is 85083 m. The loss coefficient is
0.001/1000 or 0.000001 in (1/m). These numbers can be used to calculate
a Llag for the river segment 441. The time step for calculations is equal
to the number of seconds in a month or 86400*365/12=2628000. The LLag is
then 85083/0.15/2628000 = 0.2158. To get the FFlow(t) and Fflow(t-1), open
the table "fflow.dbf" and take a look. Scroll to the right until
you find the field "gc441". Let's make a calculation for t=90
so scroll all the way to the bottom of the "fflow" table and
look at the last record. You should see something like this:

Note the values for Fflow(90)=79.89 cms and Fflow(89)=159.19 cms. Now look at "pflow.dbf" to determine the local contribution to flow in the 90th month.

Pflow(90)= 5.27 cms. To estimate Tflow, the Loss needs to be computed. The Loss in segment i is estimated as Fflow(i,t)*Length(i)*LossC(i) or 79.89*85083.26*0.000001=6.80. With all of this information, Tflow can be computed: Tflow = 159.19*(0.2158)+79.89*(1-0.2158)+5.27-0-6.80 = 95.5 cms. You can check this value by looking in the Table "Tflow.dbf."

The value in the table is 94.03. The main reason for the difference in the numbers is that the precision of the numbers presented in the Tables is less than the precision of the numbers stored in memory by the computer and thus the precision of numbers used to make the calculations.
In addition to the time-series bar charts we have looked at for selected
polygons, another way to look at the results is to make a longitudinal
profile plot. To do this, select ![]() ,
enter 0 and click OK. Click on one of the headwater arcs in the
river network and choose NO to measure distance from the selected arc to
the furthest downstream outlet. The program traces a path from the selected
arc to the furthest downstream arc and then plots a graph of mean monthly
flows in each reach. The bar chart shows two values for each watershed,
the flow value at the from-node and the flow value at the to-node. The
x-axis labels are the from-node ID numbers. An example is provided here
to aid in interpreting this plot.
,
enter 0 and click OK. Click on one of the headwater arcs in the
river network and choose NO to measure distance from the selected arc to
the furthest downstream outlet. The program traces a path from the selected
arc to the furthest downstream arc and then plots a graph of mean monthly
flows in each reach. The bar chart shows two values for each watershed,
the flow value at the from-node and the flow value at the to-node. The
x-axis labels are the from-node ID numbers. An example is provided here
to aid in interpreting this plot.

In the Chart shown, of the values labeled 118, the first is the flow generated upstream of river reach 1, the second value is the "to" flow from river reach 1. The third value shows that there is a jump in the flow from reach 1 to reach 2. This is due to tributaries joining the flow. The from-node and to-node values on river reaches 2 and 3 indicate that these two basins have more losses than locally generated flow.
Some additional tools are available for adding flow check points and
water diversions to the model. To do this, click on the red flag ![]() .
Enter 1 to add flow check points, click OK, and select YES to start
a new set. Now click on a few points in the river network where you would
like to know the mean monthly flow. Enter an ID for each point at the message
window. Click on the green flag
.
Enter 1 to add flow check points, click OK, and select YES to start
a new set. Now click on a few points in the river network where you would
like to know the mean monthly flow. Enter an ID for each point at the message
window. Click on the green flag ![]() to calculate the interpolated flow values at selected points. If one of
your selected points is not not close enough to a river line, you will
get an error message, but the interpolation program will still work on
other points in the selected set that are close enough to a river line.
If you find it difficult to select points close to the river lines, try
zooming in on an area before selecting flow check points. The Table "Attributes
of Flowchk.shp" is automatically made active after the flows are interpolated.
In this Table, the fields "Fflow," "IFlow," and "TFlow"
provide the mean monthly from flow for that river reach, the mean monthly
interpolated flow at the check point, and the mean monthly to flow for
that river reach. The field "pcntage" is the length from the
from node to the check point divided by the total reach length. If you
don't remember which check point ID corresponds to which map location,
just highlight a record in the Table and the corresponding point in View
1 will be highlighted.
to calculate the interpolated flow values at selected points. If one of
your selected points is not not close enough to a river line, you will
get an error message, but the interpolation program will still work on
other points in the selected set that are close enough to a river line.
If you find it difficult to select points close to the river lines, try
zooming in on an area before selecting flow check points. The Table "Attributes
of Flowchk.shp" is automatically made active after the flows are interpolated.
In this Table, the fields "Fflow," "IFlow," and "TFlow"
provide the mean monthly from flow for that river reach, the mean monthly
interpolated flow at the check point, and the mean monthly to flow for
that river reach. The field "pcntage" is the length from the
from node to the check point divided by the total reach length. If you
don't remember which check point ID corresponds to which map location,
just highlight a record in the Table and the corresponding point in View
1 will be highlighted.
If you use the diversion specified here, you can follow along with a
sample calculation to see the effects of the diversion. To demonstrate
the capability to add a constant flow rate diversion to the model, click
on the ![]() again and this time enter
0 to add a diversion point and select YES to start a new set. Enter
a diversion of 50 cms at some point on the river reach with grid-code 441
-- choose this so that you will be able to see how the numbers in the table
"tflow.dbf" for gc441 and time step 90 change from the example
calculation above. See figure below.
again and this time enter
0 to add a diversion point and select YES to start a new set. Enter
a diversion of 50 cms at some point on the river reach with grid-code 441
-- choose this so that you will be able to see how the numbers in the table
"tflow.dbf" for gc441 and time step 90 change from the example
calculation above. See figure below.

To see the effects of this diversion on the simulation results, you need to re-run the simulation model. To make another simulation run, select the menu item SFwModel/SFlowSim and choose all of the default parameters. When this simulation is complete, you can take a look at the effects the diversion had on the calculations by looking at the table "tflow.dbf" to see that the to flow in month 90 for grid-code 441 is now only 44.03 cms, rather than 94.03 cms from the previous calculation. Another way to see the effects of the diversion is to look at the longitudinal profiles before and after the diversion is added. You will not be able to make this comparison directly because charts are automatically updated when the tables that they reference change. Here are some graphs that show the effects of a 50 cms diversion on the profile shown.



Before running the optimization routine, let's remove any diversion
points that have been placed in the model. To do this, click on ![]() ,
enter 0, click OK, and click YES. Don't click on any points in View1. An
optimization routine can be run which varies model parameters to produce
a close fit with observed data at the Koulikoro gaging station. Model parameters
that can be optimized include the fraction of subwatershed surplus that
goes to the subsurface reservoir, the mean residential time of water in
a subsurface reservoir, the overland flow velocity, the overland flow loss
coefficient, the river flow velocity, and the river loss coefficient. In
this example, only the river flow velocity (V) and river loss coefficient
(LossC) will be varied to fit observed data. The optimization routine attempts
to minimize the root mean squared error (RMSE) by varying the river flow
velocity and forces the sum of mass differences (SMD) to zero by varying
the loss coefficient. The mathematical definitions of these terms are:
,
enter 0, click OK, and click YES. Don't click on any points in View1. An
optimization routine can be run which varies model parameters to produce
a close fit with observed data at the Koulikoro gaging station. Model parameters
that can be optimized include the fraction of subwatershed surplus that
goes to the subsurface reservoir, the mean residential time of water in
a subsurface reservoir, the overland flow velocity, the overland flow loss
coefficient, the river flow velocity, and the river loss coefficient. In
this example, only the river flow velocity (V) and river loss coefficient
(LossC) will be varied to fit observed data. The optimization routine attempts
to minimize the root mean squared error (RMSE) by varying the river flow
velocity and forces the sum of mass differences (SMD) to zero by varying
the loss coefficient. The mathematical definitions of these terms are:
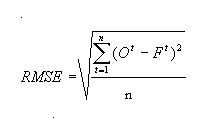


To run the optimization routine, make the Themes Ngriver.shp, Ngbasin.ply,
and Mrunoff active and use ![]() to
select all features in these coverages. Click on
to
select all features in these coverages. Click on ![]() .
Select Ngriver.shp as the Theme on which results will be matched and click
OK. A window titled "Location of gaging station as a fraction of reach
length." will come up and a default value of 0.814 is given. Just
click OK. The value 0.814 defines the location of the gaging station along
the river line in which it falls as measured from the upstream end. You
will see a message asking you to "Select a control file or click cancel
to create a new control file." A control file has been prepared for
you. Find the file c:\ngflow\ex5af.ctl and click OK. The next window tells
you which parameters are being optimized using this control file. These
parameters are the river velocity and the river loss coefficient. Parameter
bounds are specified in the control file for this run. The bounds on velocity
are 0.05 m/s and 0.4 m/s while the bounds on the loss parameter are 0.0001
and 0.0015. Click OK, OK, and OK.
.
Select Ngriver.shp as the Theme on which results will be matched and click
OK. A window titled "Location of gaging station as a fraction of reach
length." will come up and a default value of 0.814 is given. Just
click OK. The value 0.814 defines the location of the gaging station along
the river line in which it falls as measured from the upstream end. You
will see a message asking you to "Select a control file or click cancel
to create a new control file." A control file has been prepared for
you. Find the file c:\ngflow\ex5af.ctl and click OK. The next window tells
you which parameters are being optimized using this control file. These
parameters are the river velocity and the river loss coefficient. Parameter
bounds are specified in the control file for this run. The bounds on velocity
are 0.05 m/s and 0.4 m/s while the bounds on the loss parameter are 0.0001
and 0.0015. Click OK, OK, and OK.
This process takes a while so you probably want to take a BREAK.
When the optimization routine is complete, click OK and you will see four charts pop up. The chart titled "massfit.cht" shows the simulated values ("bestmass") next to the observed values ("target") for 90 months. The chart titled "mflowfit.cht" shows the same comparison of 12 mean monthly values: simulated ("mflowfit") vs. observed ("target"). The notation at the top of these charts is a bit confusing but can be explained with the following figure.

Thus, for the results of this run, the optimization routine found that a velocity of 0.203 m/s and a river loss coefficient of 0.00099 (1/km) gave the best fit. The charts "optmass.cht" and "optrmse.cht" show how SMD and RMSE varied with iteration. Values along the x-axis represent the iteration number and values on the y-axis are SMD and RMSE respectively at these iterations.
These materials may be used for study, research, and education, but please credit the authors and the Center for Research in Water Resources, The University of Texas at Austin. All commercial rights reserved. Copyright 1997 Center for Research in Water Resources.